之前我们介绍了 BJH 理论的修正方法，为吸附层厚度计算开了个头。在我们 part 2 中，将为大家详细介绍几种 t-plot 和 BJH 方法中常用到的吸附层厚度计算模型。

点击此处回顾内容：

大家知道，对于有孔材料，吸附层厚度不再随吸附量的递增而简单线性上升，比如以下微孔和介孔的 t-plot 图。

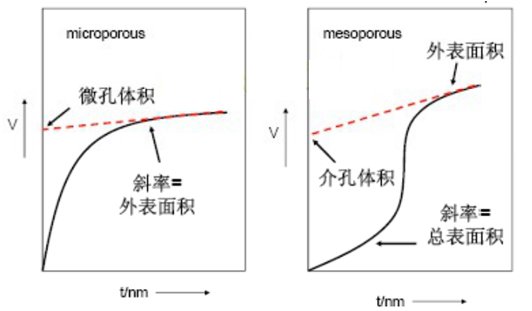
图1. 微孔与介孔 t-plot 图

这些吸附层厚度随吸附量变化的曲线是依据几个吸附层厚度计算模型得出的，大家在part 1 中应该已经见过了（见下图红框内）：

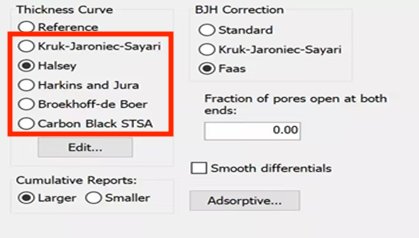
图2. 软件自带膜厚计算模型

其中 Reference 是用户自定义吸附厚层度与相对压力 p/p⁰ 的关系，由于 p/p⁰ 和平衡吸附量的关系由等温吸附曲线描述，故吸附厚度层与平衡吸附量的关系也既得出。Kruk-Jaroniec-Sayari（KJS）方法在 Part 1 中已介绍过，这里 KJS 吸附层厚度模型也是用于对 BJH 方法修正的 KJS 方法之中，可针对 MCM-41、SBA-15 类型材料的孔结构分析。

Halsey 方程是 BJH 方法中最常用的吸附层膜厚计算模型，此模型假设单层吸附液膜和液态吸附质有着相同的密度和堆积方式，并且适用于较高的相对压力区域（多层吸附区域）的分析。

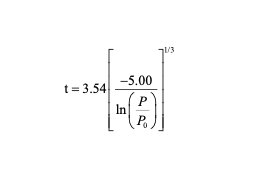
其中 t 为吸附层液膜厚度，3.54 和 5.00 为经验数值，指数 1/3 由 Lennard-Jones 势函数积分后推导出。

而 Harkins & Jura 方法对于凝聚的吸附质先建立起了相对压力和平衡吸附量的线性关系：

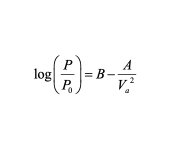
有上述线性关系可以得到 A 与 B 值。对于不同的吸附剂-吸附质体系，A、B 值各不同，一般经验上取 A 为 13.99，B 为 0.034 带入如下吸附层厚度计算公式：

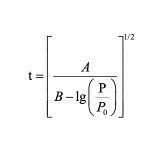
Broekhoff-de Boer 理论假设吸附层厚度的增减不仅与吸附质相对压力的大小有关，还与达到稳定平衡的吸附层自身化学势有关。平坦吸附剂表面稳定的吸附层化学势比液化的吸附质化学势要低，其两者差值由函数 F(t) 描述，而且在达到平衡时，平坦表面吸附的吸附质化学势与气态吸附质化学势相等，所以我们可以得出：

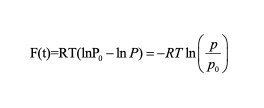
对于氧化物，氢氧化物材料的多层氮气吸附，当吸附层厚度大于 5 埃时，我们有 Broekhoff-de Boer 经验式：

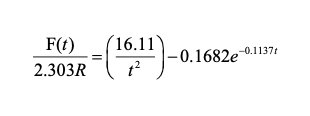
这样，我们就将 F(t) 与相对压力（p/p₀）和吸附层厚度 t 联系了起来，从而可以绘制 t-plot 曲线。对于介孔中存在弯曲液面的情况，吸附剂孔道表面稳定的吸附层化学势与宏观液化的吸附质化学势的差值- RTln（p/p₀）可以等于：

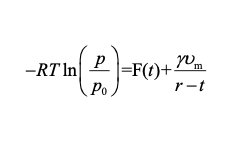
（对于圆柱形孔）

或

（对于球形孔）

其中 γ 为吸附层的表面张力，ν_m 为吸附质气体的摩尔体积，r 为孔半径，t 为吸附层厚度。

最后，carbon black STSA（Statistical Thickness Surface Area）是一个测量炭黑材料总表面积和外表面积国际标准，是结合了炭黑材料本身特性和 Broekhoff-de Boer 理论的方法。这个方法先用 BET 方法测量炭黑材料的总表面积，然后可利用 Broekhoff-de Boer 理论绘制炭黑材料的 t-plot 图，通过 t-plot 图上平坦区域的斜率得出炭黑材料的外表面积，最后就可算出炭黑材料的内表面积和总孔体积。

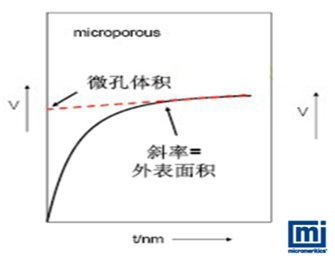
图3. 微孔t-plot图（如多微孔炭黑）

相信到这里，大家对吸附层厚度计算公式及理论已经有了一定的了解，下次选择对材料进行 t-plot 和 BJH 方法分析时，可不要选错了吸附层厚度计算模型哦。